Física quântica exige números complexos - e sempre terá uma parte imaginária
Redação do Site Inovação Tecnológica - 17/12/2021

[Imagem: Georgy Ermakov/Sergey Lebedyanskiy]
Parte imaginária da Física
Uma equipe internacional de pesquisadores demonstrou, por meios teóricos e experimentais, que a teoria quântica não pode ser expressa usando números reais, ratificando sua necessidade intrínseca dos números complexos.
O problema é que os números complexos têm uma parte real e uma parte imaginária.
Historicamente, os físicos vinham considerando que os números complexos eram meramente uma ferramenta conveniente para a mecânica quântica - e não uma parte necessária dela.
Contudo, Marc-Olivier Renou e seus colegas da Áustria, Espanha e China demonstraram agora que, se os postulados quânticos fossem formulados em termos de números reais - em vez de números complexos - então algumas previsões sobre as redes quânticas seriam necessariamente diferentes.
Ou, dito de outra forma, uma previsão feita pela teoria quântica padrão, usando números complexos, não pode ser expressa por sua contraparte real.
Física dos números reais
Os cientistas constroem teorias para descrever a natureza, e depois usam essas teorias para fazer previsões sobre como a natureza irá se comportar. A seguir, eles constroem modelos, que são idealizações simplificadas de uma natureza que seguisse unicamente aquela teoria, para facilitar a realização de experimentos do tipo "O que aconteceria se...".
Digamos que você queira fazer uma trilha em uma montanha desconhecida. Para evitar ficar perdido, você usa um mapa. O mapa é uma representação da montanha, com suas florestas, encostas, trilhas etc. Mas o mapa não é a montanha - o mapa é um modelo, construído seguindo a teoria de que é possível representar a realidade tridimensional da montanha em um papel bidimensional.
As teorias da Física não são expressas na forma de mapas, mas em termos de objetos matemáticos, como equações, integrais ou derivadas. Conforme essas teorias foram evoluindo, para descrever fenômenos mais complicados, elas passaram a utilizar conceitos matemáticos igualmente mais complicados.
Mas uma fronteira foi cruzada no início do século XX, quando a teoria quântica surgiu: Entre as muitas mudanças drásticas que ela trouxe, sua complicação extrema fez com que ela se tornasse a primeira teoria científica formulada em termos de números complexos.
Inventados por matemáticos há séculos, os números complexos são compostos por uma parte real e uma parte imaginária. Foi Descartes, o filósofo considerado o pai das ciências racionais, quem cunhou o termo "imaginário", para contrastar fortemente essa nova expressão numérica com o que ele chamou de números "reais".
Apesar de seu papel fundamental na matemática, não se esperava que os números complexos tivessem um papel semelhante na Física por causa dessa parte imaginária. E, de fato, antes da teoria quântica, a mecânica de Newton ou o eletromagnetismo de Maxwell usavam números reais para descrever, digamos, como os objetos se movem ou como os campos eletromagnéticos se propagam - as teorias às vezes empregavam números complexos para simplificar alguns cálculos, mas seus axiomas só faziam uso de números reais.
[Imagem: Marc-Olivier Renou et al. - 10.1038/s41586-021-04160-4]
Introdução dos números complexos na Física
A teoria quântica desafiou radicalmente esse estado de coisas porque seus postulados fundamentais foram formulados em termos de números complexos. A nova teoria, embora muito útil para prever os resultados dos experimentos - por exemplo, os níveis de energia do átomo de hidrogênio - ia contra a intuição em favor dos números reais.
Procurando uma descrição dos elétrons, Erwin Schrodinger (1887-1961) foi o primeiro a introduzir números complexos na teoria quântica por meio de sua famosa equação, que trata da função de onda, um objeto matemático que especifica o comportamento dos elétrons em uma molécula - hoje a função de onda é considerada uma realidade, e não apenas um construto matemático.
No entanto, Schrodinger não conseguia conceber que os números complexos pudessem realmente ser necessários na Física nesse nível fundamental. Era como se ele tivesse encontrado um mapa para representar as montanhas, mas esse mapa fosse na verdade composto por desenhos abstratos e não-intuitivos. Tamanha foi sua perplexidade que ele escreveu uma carta a Hendrik Lorentz (1853-1928) em 6 de junho de 1926, declarando: "O que é desagradável aqui, e na verdade deve ser objetado diretamente, é o uso de números complexos. Ψ certamente é fundamentalmente uma função real" - a letra grega psi (Ψ) é utilizada para representar a função de onda na mecânica quântica.
Para reforçar essa crença, em 1960 o professor Ernst Stueckelberg [1905-1984], da Universidade de Genebra, na Suíça, demonstrou que todas as previsões da teoria quântica para experimentos de partícula única poderiam ser igualmente derivadas usando apenas números reais. Desde então, o consenso era que os números complexos na teoria quântica eram apenas uma ferramenta conveniente.
[Imagem: Zheng-Da Li et al. (2021)]
Implicações físicas e filosóficas
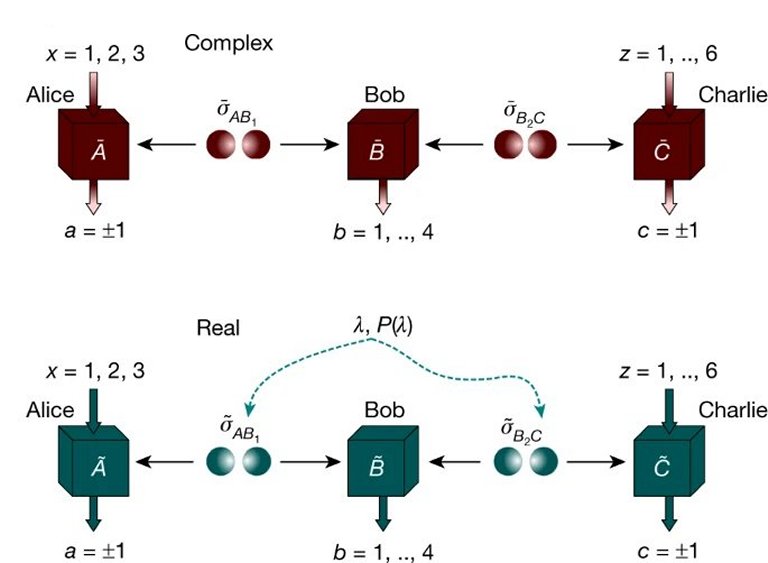
Quando tudo parecia tão calmo e estabelecido, eis que Marc Renou e seus colegas decidiram jogar gasolina nessa fogueira quase apagada: Eles, a princípio idealizaram um experimento mental de redes quânticas e demonstraram que os resultados previstos pela teoria usando números reais era diferente das previsões feitas usando os números complexos.
Para isso, eles pensaram em um cenário específico que envolve duas fontes independentes (S e R), colocadas entre três nós de medição (A, B e C) em uma rede quântica elementar. A fonte S emite duas partículas, digamos fótons, uma para A e a segunda para B. Os dois fótons são preparados em um estado emaranhado, digamos em polarização. Ou seja, eles correlacionaram a polarização de uma maneira que é permitida pela teoria quântica (complexa e real), mas que é impossível classicamente (não existe entrelaçamento na teoria clássica).
A fonte R faz exatamente o mesmo, emite dois outros fótons preparados em um estado emaranhado e os envia para B e C, respectivamente. O ponto-chave neste experimento mental foi encontrar a forma adequada de medir esses quatro fótons nos nós A, B e C, a fim de obter previsões que não pudessem ser explicadas quando a teoria quântica está restrita a números reais. Não deu certo.
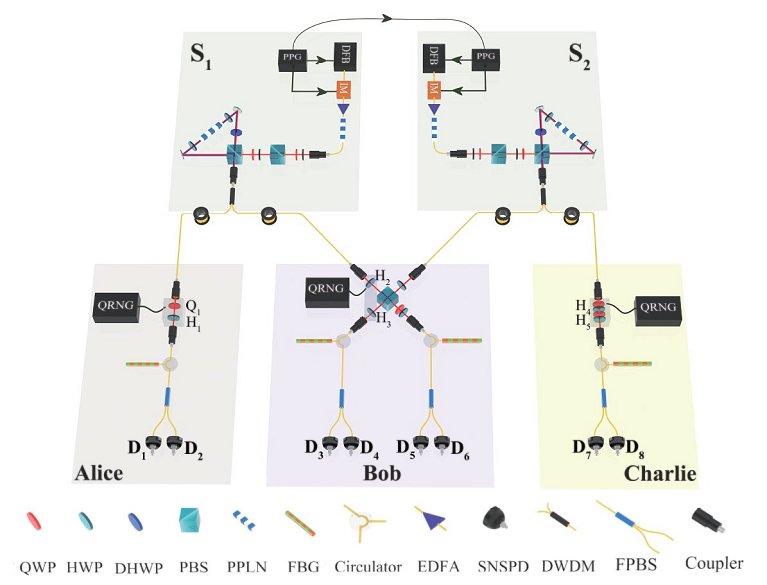
"Quando chegamos a esse resultado, o desafio era ver se nosso experimento mental poderia ser feito com as tecnologias atuais. Depois de discutir com colegas de Shenzhen-China, encontramos uma maneira de adaptar nosso protocolo para torná-lo viável com seus dispositivos de última geração. E, como esperado, os resultados experimentais correspondem às previsões!" contou Renou.
Estes resultados já estão ecoando pela comunidade científica, mas não se espera deles uma consequência direta e única. De fato, a expectativa é que as implicações ecoem não apenas dentro da Física, mas também da Matemática e da Filosofia: Será que a tão exata Física tem em sua própria essência um componente imaginário?
Artigo: Quantum theory based on real numbers can be experimentally falsified
Autores: Marc-Olivier Renou, David Trillo, Mirjam Weilenmann, Le Phuc Thinh, Armin Tavakoli, Nicolas Gisin, Antonio Acín, Miguel Navascues
Revista: Nature
DOI: 10.1038/s41586-021-04160-4
Artigo: Testing real quantum theory in an optical quantum network
Autores: Zheng-Da Li, Ya-Li Mao, Mirjam Weilenmann, Armin Tavakoli, Hu Chen, Lixin Feng, Sheng-Jun Yang, Marc-Olivier Renou, David Trillo, Thinh P. Le, Nicolas Gisin, Antonio Acín, Miguel Navascues, Zizhu Wang, Jingyun Fan
Revista: Physical Review Letters


LEDs finos como fios de cabelo podem substituir os lasers
Mineração espacial será feita por bactérias e fungos
Resfriamento barocalórico oferece novo caminho para a refrigeração
Sinapse artificial de luz impulsiona computação neuromórfica
Armazenar dados em DNA é mais fácil do que se pensava
Lente plana gera uma imagem para a frente e outra para trás
Baterias "macias" podem fazer a ponte entre as atuais e as sólidas
Computação com luz é ótimo, mas como fazer a luz pensar em números negativos?
Chip quântico acomoda até 2 milhões de qubits por mm2
Energia das ondas é extraída com eficiência ótima usando giroscópios
Chip quântico acomoda até 2 milhões de qubits por mm2
Refrigeração criogênica é feita com metais comuns, sem terras raras
Tempo quântico pode ser medido sem um relógio
Cristal do tempo levita e desafia Terceira Lei de Newton
Buracos de minhoca não existem, Big Bang é um portal e o tempo vai e vem, propõem físicos
Luz é focalizada e desfocada no espaço livre, sem lentes
Todos os direitos reservados.
É proibida a reprodução total ou parcial, por qualquer meio, sem prévia autorização por escrito.




